2018-04-25 • algorithm c parallel

双调排序的并行实现

双调排序是比较顺序与数据无关的排序方法，特别适合做并行计算，例如用GPU、FPGA来计算。当要排序的数的个数不是2的幂时，处理时较为困难。本文介绍了一种非padding的解决方案。

算法实现目标

给出分成m段的n个浮点数，输入数据已按段号有序，但每段内部无序。用C/C++ 编写一个分段双调排序(Bitonic sort)函数，对每一段内部的浮点数进行排序，但不要改变段间的位置。

接口方式:

void segmentedBitonicSort(float* data, int* seg_id, int* seg_start, int 
n, int m);

// 输入数据中，data包含需要分段排序的n个float值，seg_id给出data中n个元素各自所在的 段编号。
// seg_start共有m+1个元素，前m个分别给 出0..m-1共m个段的起始位置，seg_start[m]保证等于n。

// seg_id中的元素保证单调不下降，即对任意的i<j，seg_id[i]<=seg_id[j]。seg_id所有元 素均在0到m-1范围内。

// 输出结果覆盖data，保证每一段内排序，但不改变段间元素的顺序。

样例输入：

float data[5]={0.8, 0.2, 0.4, 0.6, 0.5};
int seg_id[5]={0,   0,   1,   1,   1};
int seg_start[3]={0,2,5};
int n=5;
int m=2;

样例输出：

float data[5]={0.2, 0.8, 0.4, 0.5, 0.6};

加分要求（不要求全部实现）：

1、不递归：segmentedBitonicSort函数及其所调用的任何其他函数都不得直接或间接地进行递归。

2、不调用函数：segmentedBitonicSort不调用除标准库函数外的任何其他函数。

3、内存高效：segmentedBitonicSort及其所调用的任何其他函数都不得进行动态内存分配，包括malloc、new和静态定义的STL容器。

4、可并行：segmentedBitonicSort涉及到的所有时间复杂度O(n)以上的代码都写在for循环中，而且每个这样的for循环内部的循环顺序可以任意改变，不影响程序结果。注：自己测试时可以用rand()决定循环顺序。

5、不需内存：segmentedBitonicSort不调用任何函数（包括C/C++标准库函数），不使用全局变量，所有局部变量都是int、float或指针类型，C++程序不使用new关键字。

6、绝对鲁棒：在输入数据中包含NaN时（例如sqrt(-1.f)），保证除NaN以外的数据正确排序，NaN的个数保持不变。

算法描述

基础定义

双调序列(Bitonic Sequence)是指由一个非严格增序列X和非严格减序列Y构成的序列，比如序列(23,10,8,3,5,7,11,78)。

定义：一个序列 a_1,a_2,…,a_n 是双调序列(Bitonic Sequence)，如果：

存在一个a_k (1≤k≤n), 使得a1≥⋯≥ak≤⋯≤an成立；或者
序列能够循环移位满足条件1

双调划分

首先我们定义一个操作是sortSeq, 输出是一个双调序列，其中前半段s_1是升序，后半段s_2是降序，设这个序列的长度是n,那么s_1的元素是[a_0, a_1, … ,a_(n/2-1)], s_2的元素是[a_(n/2), a_(n/2+1), … , a_n].

对s_1和s_2按照元素的对应位置进行如下操作：

如果a_0 ≤ a_(n/2), 那么不进行操作，否则交换两个元素.

用形式化的表示就是：

双调序列构建

算法采用从低向上的方法逐步构建双调序列

对于无序数组 A，相邻的两个数肯定是双调序列，比如(a0,a1), (a2,a3)等等. 首先对a0,a1传入sortSeq，变成升序序列，a2,a3传入sortSeq，变成降序序列，a4,a5变成升序序列….. 接下来步长变为4，a0,a1,a2,a3是双调序列，传入sortSeq变成升序序列，a4,a5,a6,a7也是双调的，传入sortSeq变成降序序列

对16个数的排序过程：

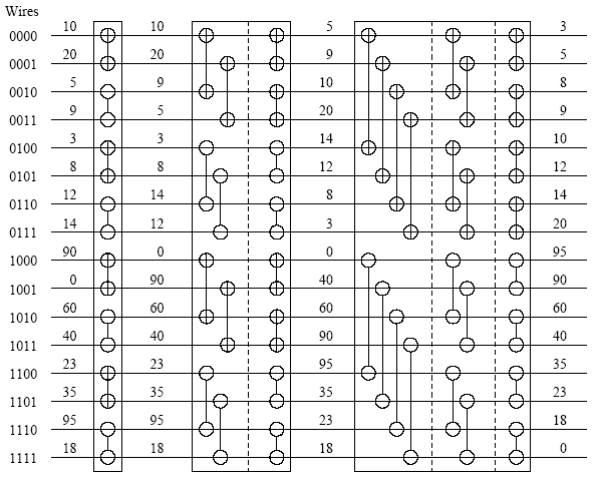
上图中排序函数调用分析：

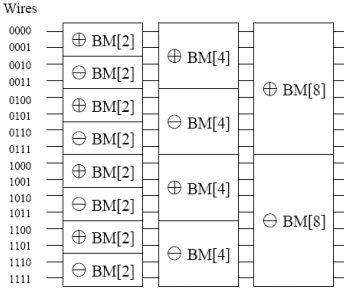
最后步长是n，前n/2元素是升序，后n/2是降序，传入sortSeq变成升序序列。至此算法完成。

原理和证明参考：《Bitonic Sort: Overview》

n!=2^k的双调排序网络

n!=2^k时，可以采用padding的方法，但是需要额外空间，这里使用另一种方法。标准的双调排序使用了比较网络B_p （p=2^k），我们根据比较网络B_p推导出对于任意n的网络B_n，p是大于的第一个2的幂次方，然后仅仅对n-p/2的元素使用比较网络。图3展示了n=6时的比较网络B_n，把它嵌入到p=8的比较网络B_p，仅仅使用了前两个比较器。

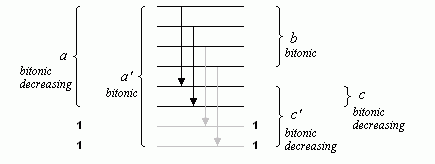
通过将一个双调递减的序列使用上述方法可以得到一个递增的序列。通过将一个双调递增的序列使用上述方法可以得到一个递减的序列。

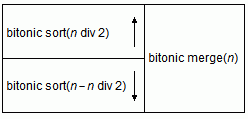
当n=13时，该算法的比较网络如下图：

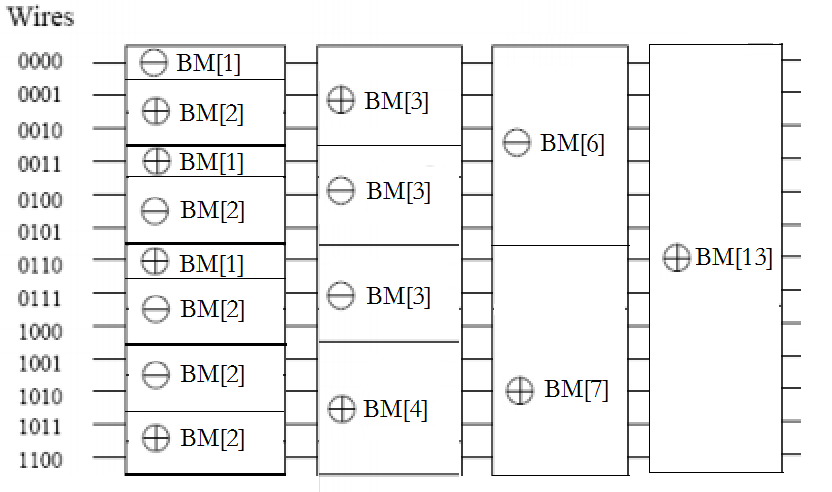
非递归实现时，先用二分的方法计算出网络结构和每一个BM的方向，存储在seg_id中，之后从深到浅，依次处理每一个BM过程。

做法正确性论述请看：《Bitonic sorting network for n not a power of 2》

测试数据

数据1：

    float data[12]={0.8,sqrt(-1.f),sqrt(-1.f),0.5,0,0,-1,sqrt(-1.f),3453,0,-1,0};
    int seg_id[12]={0,0,0,0,1,1,1,1,1,1,2,2};
    int n=12;
    int m=3;
    int seg_start[4]={0,4,10,12};

结果：

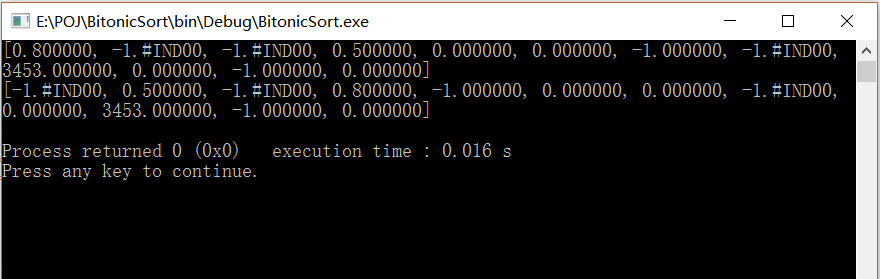
数据2：（对n从1-16分别进行测试）

    ElemType data[16] = {10,20,5,9,3,8,12,14,90,0,60,40,23,35,95,18};
    int seg_id[16] =    {0, 0, 0,0,0,0, 0, 0, 0,0, 0, 0, 0, 0, 0, 0};
    int seg_start[2] = {0,16};
    int m=1;
    int n = 16;

结果：

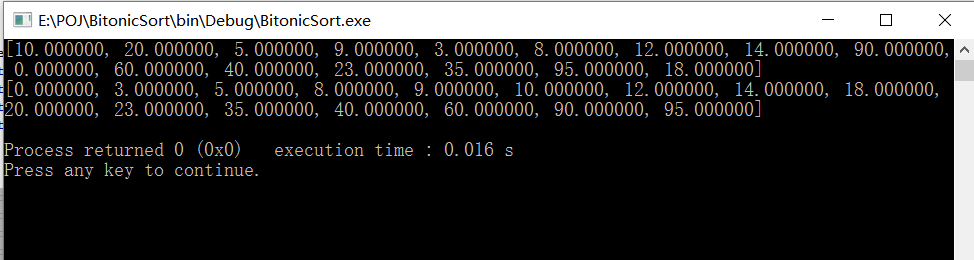
数据3：

    float data[5]={0.8, 0.2, 0.4, 0.6, 0.5};
    int seg_id[5]={0,   0,   1,   1,   1};
    int seg_start[3]={0,2,5};
    int n=5;
    int m=2;

结果：

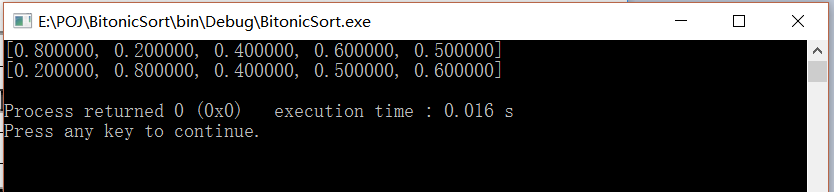
实现参考

Flensburg大学的JAVA版本的代码，这个代码使用递归方式解决问题。支持n不为2的幂次方的输入。
Rutgers大学的c代码, 这个代码没有递归，但在处理n不为2的幂次方的输入时遇到了问题。
CSDN上boboanan==博主的代码，博客中的要求一样。他用一个vector将数据存下来，并将数据补齐到2的幂的长度。

最后根据Flensburg大学提供的思路，用非递归的方式完成了双调排序，实现了所有加分挑战。

代码

#include <stdio.h>
#include <math.h>

//#define DEBUG

typedef float ElemType;

void printArray(ElemType *arr, int n) {
    int i;
    printf("[%f",arr[0]);
    for (i=1; i < n;i++) {
        printf(", %f",arr[i]);
    }
    printf("]\n");
}

void printBinary(int n)
{
    int i;
    for(i=8; i>=0;i--){
        printf("%d",(n>>i)&1);
    }
}

void segmentedBitonicSort(float* data, int* seg_id, int* seg_start, int n, int m)
{/* data包含需要分段排序的n个float值，
    seg_id给出data中n个元素各自所在的段编号。
    seg_start共有m+1个元素，前m个分别给出0..m-1共m个段的起始位置，seg_start[m]保证等于n。*/
    int seg_no;
    for(seg_no=0; seg_no<m; seg_no++){
        /// 计算出每一个段的起始位置，长度，seg_id对应位置
        float *arr = &data[seg_start[seg_no]];
        int *arr_id = &seg_id[seg_start[seg_no]];
        int length = seg_start[seg_no+1] - seg_start[seg_no];
        /// 对一个单独的段使用双调排序算法
        //BitonicSort(A, length，id);
        {// 这一段用大括号括起来，可以作为一个单独的函数
            /// 先构建bitonic sorting network，利用位运算将network信息存储到seg_id中
            int loop_change_flag;
            int hb0,hbi,hbj,hb_len,hb_middle;
            // 使用一个二进制位记录bitonic merge过程的方向，1为升序，0为降序

            for(hbj=0;hbj<length;hbj++){
                arr_id[hbj] = arr_id[hbj]<<1 | 0x01;
            }
            // 每次除以2，将数组切分，并计算每个BM过程的方向，存入seg_id
            loop_change_flag = 1;
            hb0 = 0;
            while(loop_change_flag){
                loop_change_flag = 0;
                for(hbi=hb0; hbi<length&& arr_id[hbi]==arr_id[hb0]; hbi++);
                hb_len = hbi - hb0;
                hb_middle = hb_len/2;
                if(hb_len>=2){
                    loop_change_flag = 1;
                    for(hbj=hb0; hbj < hb0+hb_middle; hbj++){
                        arr_id[hbj] = arr_id[hbj]<<1 | !(arr_id[hbj]&0x01);
                    }
                    for(hbj=hb0+hb_middle; hbj < hb0+hb_len; hbj++){
                        arr_id[hbj] = arr_id[hbj]<<1 | (arr_id[hbj]&0x01);
                    }
                }
                hb0 = hbi;
                if(hbi==length)
                    hb0 = 0;
            }
            #ifdef DEBUG
            for(hbj=0;hbj<length;hbj++){
                printBinary(arr_id[hbj]);
                printf(" ");
            }
            #endif // DEBUG

            // do merges
            /// 循环处理所有BM过程，方向已由seg_id确定
            int cur_array_offset;
            int direction;
            int step;
            float temp, *cur_array;
            int min_power_of_2;
            for(hb0 = 0; hb_len < length;){
                // 找出一个BM过程
                for(hbi=hb0; hbi<length&& arr_id[hbi]==arr_id[hb0]; hbi++);
                hb_len = hbi - hb0;
                if(hb_len>=2){
                    // 计算这个BM过程需要使用多大的Bp网络
                    min_power_of_2=1;
                    while (!(min_power_of_2>=hb_len)){
                        min_power_of_2 = min_power_of_2<<1;
                    }

                    cur_array = arr+hb0;
                    cur_array_offset = hb0;
                    // 计算排序方向
                    direction = (arr_id[cur_array_offset] & 0x01 );

                    /// 开始一个Bitonic Merge过程
                    //merge_order((arr+block_start), min_power_of_2, hb_len, direction);
                    int i,j,k;
                    #ifdef DEBUG
                    printf("\n\n %cBM%d, offset:%d", direction?'+':'-', hb_len, cur_array_offset);
                    #endif // DEBUG

                    for (step = min_power_of_2/2; step>0; step/=2) {
                        #ifdef DEBUG
                        printf("\n STEP %d : ", step);
                        #endif // DEBUG
                        for (i=0; i < min_power_of_2; i+=step*2) {
                            for (j=i,k=0; k < step; j++,k++) {
                                if (cur_array_offset+j+step>=hb0+hb_len)
                                    continue;
                                #ifdef DEBUG
                                printf("check %d(%.1f), %d(%.1f). ", cur_array_offset+j, cur_array[j], cur_array_offset+j+step, cur_array[j+step]);
                                #endif // DEBUG
                                if ( direction == (cur_array[j] > cur_array[j+step])) {
                                    // swap
                                    temp = cur_array[j];
                                    cur_array[j] = cur_array[j+step];
                                    cur_array[j+step] = temp;
                                    #ifdef DEBUG
                                    printf("swap. ");
                                    #endif // DEBUG
                                }
                            }
                        }
                    }
                }
                // 删除此次排序的id信息
                for(hbj=hb0; hbj < hb0+hb_len; hbj++){
                    arr_id[hbj] = arr_id[hbj]>>1;
                }
                // 一次排序完成后,开始下一次排序.一层结束后，开始下一层.
                hb0 = hbi;
                if(hbi==length)
                    hb0 = 0;
                #ifdef DEBUG
                printf("\n ## ");
                printArray(arr, length);
                #endif // DEBUG
            }
        }
    }
}

int main()
{
    // test input 1
/*
    ElemType data[16] = {10,20,5,9,3,8,12,14,90,0,60,40,23,35,95,18};
    int seg_id[16] =    {0, 0, 0,0,0,0, 0, 0, 0,0, 0, 0, 0, 0, 0, 0};
    int seg_start[2] = {0,16};
    int m=1;
    int n = 16; // number of numbers to be sorted
*/
    // test input 2
/*
    float data[12]={0.8,sqrt(-1.f),sqrt(-1.f),0.5,0,0,-1,sqrt(-1.f),3453,0,-1,0};
    int seg_id[12]={0,  0,         0,         0,  1,1, 1,1,         1,   1,2,2};
    int n=12;
    int m=3;
    int seg_start[4]={0,4,10,12};
*/
    // sample input

    float data[5]={0.8, 0.2, 0.4, 0.6, 0.5};
    int seg_id[5]={0,   0,   1,   1,   1};
    int seg_start[3]={0,2,5};
    int n=5;
    int m=2;


    // print array before
    printArray(data, n);

    segmentedBitonicSort(data, seg_id, seg_start, n, m);

    // output result
    printArray(data,n);

    return 0;
}

总结分析

无论是递归还是非递归，排序网络都需要 ⌈log⁡(n)⌉*(⌈log⁡(n)⌉+1)/2 级，每一级最多有 n/2 个比较器，故计算复杂度为 O(n*log^2(⁡n))。计算网络结构时和实际排序的复杂度相同，也是O(n*log^2⁡(n))，故最终计算复杂度仍为 O(n*log^2(⁡n))。考虑到可以使用并行的方式优化掉n，故速度比快速排序O(n*log⁡n)要快。

最后的实现用的不是padding的方法，但是花费了相当一部分计算量去计算网络的结构。和padding的方法相比，相当于是用时间换了空间。计算网络的结构的部分也可以并行实现，但是网络的结构没有padding的方法规整，这可能会对硬件有更高的要求。故若存储空间较大的情况下建议使用padding的方法，在空间有限的情况下再使用直接计算网络结构的方法。

沧歌